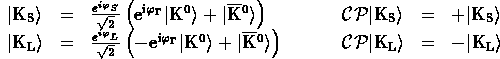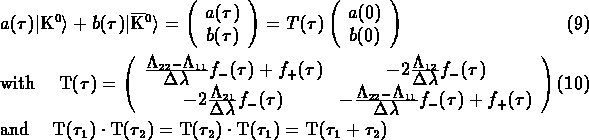
The time evolution of an arbitrary neutral kaon state after solving eq. 2 is given by:
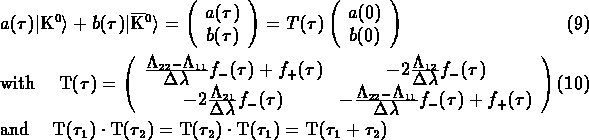
with
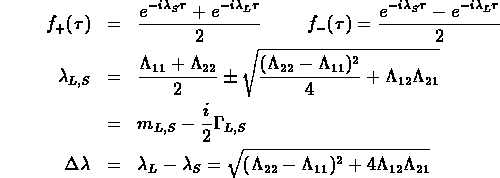
where 
and 
are the eigenvalues of the matrix 
.
The eigenvectors which follow an exponential decay law are given by:
with arbitrary phases 
, 
and
In the special case of initial pure 
or 
at time 
we obtain:
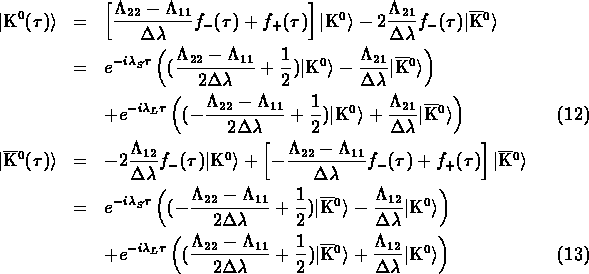
In the limit of small 
violation, i.e.
and small 
violation, i.e.
, we obtain:
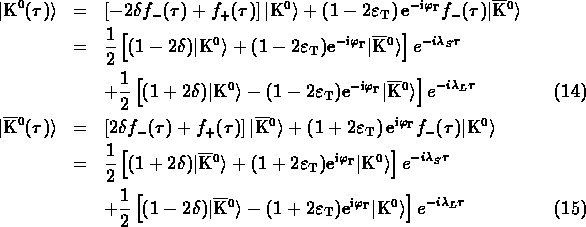
with 
and 
describing and violation
in the mass and decay matrix:
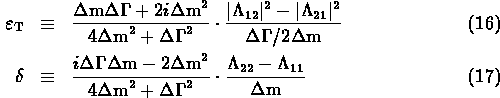
The phase of the parameter is identical to the superweak phase
.
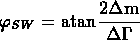The masses and decay widths of the two eigenstates are given
by 
:
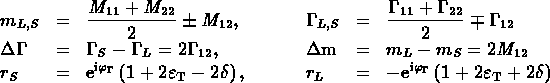
In the limit of 
conservation and by fixing the arbitrary phase
, 
and 
become eigenstates with
eigenvalues +1 and -1:
