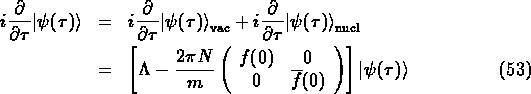
The equation of motion inside some material can be written as:
By comparing eq. 53 with the eq. 2, we can immediately write down the solutions for the time evolution of a neutral kaon state inside some material:
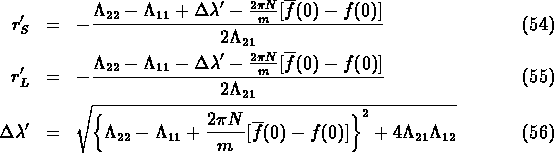
The mass and lifetime eigenvalues of 
and 
change equally in
first order of the forward scattering amplitudes.
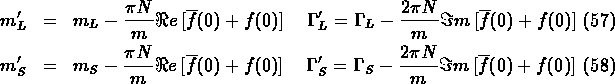
And the time evolution of a 
or 
in matter becomes:
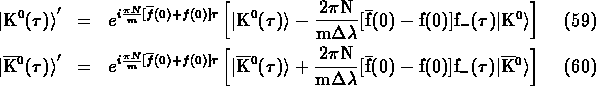
For an arbitrary inital neutral kaon state we can write following the formalism in section 1:
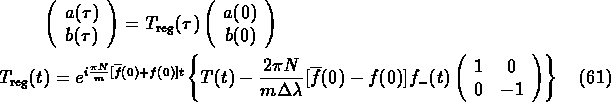
Consider the standard case of an initial pure 
:
( 
counts time after regenerator, 
time inside
regenerator):
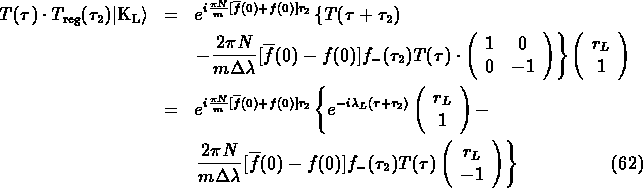
To get a more simple expression, assume 
conservation, i.e.
:
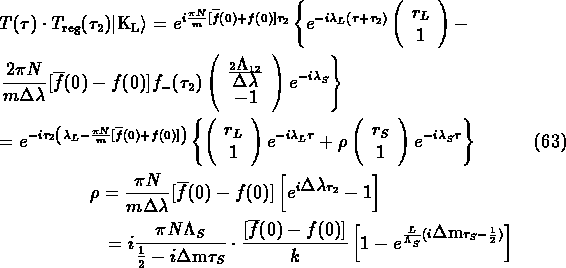
where 
, 
,
and 
.
A similar calculation yields:
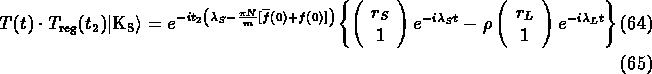
For evaluating and decays in vacuum, it is useful to rotate to
the 
basis using the transformation matrix:
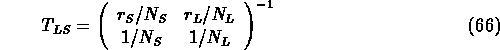
with
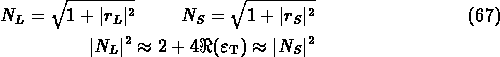
The decay rates for initial pure and into 
after
the regenerator is then given by:
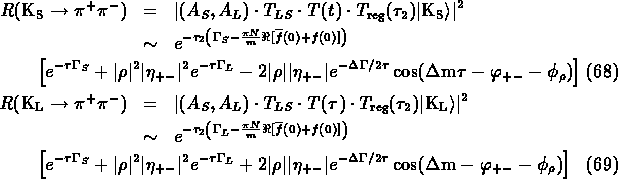
The decay rates for initial pure or after a regenerator where
the neutral kaons travel first through vacuum before reaching the regenerator
can be calculated similarly:
Moreover, the decay rate after different regenerators can be easily calculated by multiplying the corresponding matrices:
